题目描述

棋盘上 A 点有一个过河卒，需要走到目标 B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，A 点 (0, 0)、B 点 (n, m)，同样马的位置坐标是需要给出的。

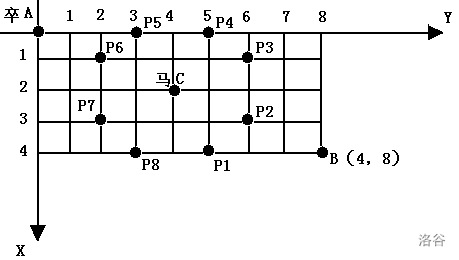
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 B 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

样例输入

6 6 3 3

样例输出

6

对于 100% 的数据，1 <= n, m <= 20，0 <= 马的坐标  <= 20。

【题目来源】

NOIP 2002 普及组第四题

题目分析

首先 A 点的坐标是(0,0)(0,0)！并且，卒只能向下或向右！

我们都清楚象棋中的马是如何跳的，跳的是“日”字形。以输入样例 6×6，马在 (3,3)(3,3) 为例，左至右分别为 x ，上至下分别为 y。

其中 C 点为马的控制点。我们不妨把马的控制点 a[x][y] 标记为 1。

样例共有 6 条路径：

大家仔细观察一下，马在第一排 (y=0)(y=0) 的走法有三种：

  1. 第一排走到底，再走到目标点；

  2. 第一排走到第四个 0 的位置，这里大家可以看出有一种路径；

  3. 第一排走到倒数第二个 0 的位置，拐个弯到达目标位置；

这里总共 33 种走法； 在第一列 (x=0)(x=0) 的走法有两种，分别是：

  1. 第一列走到倒数第二个 0 的位置，拐个弯到达目标位置；

  2. 第一列走到第四个 0 的位置，大家可以看出有一种路径；

  3. 第一列走到底，再走到目标点；

这里总共有 3 种走法；加上前面的3种，共有6种！

看到这里，大家应该明白了题意，现在我们看输入输出：

  1. 输入前两个数，为棋盘的长宽；

  2. 输入后两个数，为马的坐标(x,y)(x,y)；

代码实现

搜索回溯

一匹马

先判断出马的所有据点坐标
判断坐标是否越界
但考虑的细节很多，代码如下：

#include<bits/stdc++.h>
using namespace std;
<p>int n,m,x,y;  //(n,m)=终点坐标  (x,y)=马坐标
int sum=0; //计数
bool a[21][21]={0}; //判断是否可走</p>
<p>void dfs(int x,int y){
for(int i=1;i<=2;i++){  //有两种情况(向上或向右走)
if(x<=n&&y<=m&&a[x][y]==0){
int oldx=x,oldy=y;
if(i==1){  //向下走 防止越界 判断下面的数是否被马占领
x++;
}
if(i==2){  //向右走 防止越界 判断右边的数是否被马占领
y++;
}
if(x==n&&y==m){
sum++;
}
else{
dfs(x,y);
}
x=oldx,y=oldy;  //返回原值
}
}
}</p>
<p>int main(){</p>
<pre><code>cin&gt;&gt;n&gt;&gt;m&gt;&gt;x&gt;&gt;y;

//判断马的据点
a[x][y]=1;
// P1
if(x+2&lt;=n&amp;&amp;y+1&lt;=m){
	a[x+2][y+1]=1;
}
// P2
if(x+1&lt;=n&amp;&amp;y+2&lt;=m){
	a[x+1][y+2]=1;
}
// P3
if(x-1&gt;=0&amp;&amp;y+2&lt;=m){
	a[x-1][y+2]=1;
}
// P4
if(x-2&gt;=0&amp;&amp;y+1&lt;=m){
	a[x-2][y+1]=1;
}
// P5
if(x-2&gt;=0&amp;&amp;y-1&gt;=0){
	a[x-2][y-1]=1;
}
// P6
if(x-1&gt;=0&amp;&amp;y-2&gt;=0){
	a[x-1][y-2]=1;
}
// P7
if(x+1&lt;=n&amp;&amp;y-2&gt;=0){
	a[x+1][y-2]=1;
}
// P8
if(x+2&lt;=n&amp;&amp;y-1&gt;=0){
	a[x+2][y-1]=1;
}

dfs(0,0); 

cout&lt;&lt;sum;

return 0;

}

因为用的是搜索回溯而不是递归，所以会超时！

两匹马

偷懒思路-两匹马

偷懒思路：
这个思路是我朋友想到的（所以没加注释，应该很好懂吧）
把数组设大一点，把棋盘放到中间
这样就不用考虑越界了！代码如下：

#include<bits/stdc++.h>
using namespace std;</p>
<p>int s[10001][10001]={0},n,m,x1,y3,y2,x2,sum=0;</p>
<p>int sch(int x,int y){
for(int i=1;i<=2;i++){
if(s[x][y]==0&&x<=n+100&&y<=m+100){
int p=x,l=y;
if(i==1){
x++;
}
if(i==2){
y++;
}
if(n+100==x&&m+100==y){
sum++;
}
else{
sch(x,y);
}
x=p;
y=l;
}
}
}</p>
<p>int main(){</p>
<pre><code>cin&gt;&gt;n&gt;&gt;m&gt;&gt;x1&gt;&gt;y3&gt;&gt;x2&gt;&gt;y2;
s[x1+100][y3+100]=1; 
s[x1+100-2][y3+100+1]=1;
s[x1+100-2][y3+100-1]=1; 
s[x1+100+1][y3+100-2]=1; 
s[x1+100+1][y3+100+2]=1;  
s[x1+100-1][y3+100+2]=1;  
s[x1+100-1][y3+100-2]=1;
s[x1+100+2][y3+100-1]=1;  
s[x1+100+2][y3+100+1]=1;  
s[x2+100-2][y2+100+1]=1;
s[x2+100-2][y2+100-1]=1; 
s[x2+100+1][y2+100-2]=1; 
s[x2+100+1][y2+100+2]=1;  
s[x2+100-1][y2+100+2]=1;  
s[x2+100-1][y2+100-2]=1;
s[x2+100+2][y2+100-1]=1;  
s[x2+100+2][y2+100+1]=1;  
s[x2+100][y2+100]=1;
sch(100,100);
cout&lt;&lt;sum; 

return 0;

}

要注意的是，这种思路要从(100,100)开始
则 sch(100,100);

一般思路-两匹马

浅浅改一下代码就可以了！

#include<bits/stdc++.h>
using namespace std;</p>
<p>int n,m,xxx,yyy,xx,yy;  //(n,m)=终点坐标  (xx,yy)=第一匹马的坐标 (xxx,yyy)=第二匹马的坐标
int sum=0; //计数
bool a[21][21]={0}; //判断是否可走</p>
<p>void dfs(int x,int y){
for(int i=1;i<=2;i++){  //有两种情况(向上或向右走)
if(x<=n&&y<=m&&a[x][y]==0){
int oldx=x,oldy=y;
if(i==1){  //向下走 防止越界 判断下面的数是否被马占领
x++;
}
if(i==2){  //向右走 防止越界 判断右边的数是否被马占领
y++;
}
if(x==n&&y==m){
sum++;
}
else{
dfs(x,y);
}
x=oldx,y=oldy;  //返回原值
}
}
}</p>
<p>int main(){</p>
<pre><code>cin&gt;&gt;n&gt;&gt;m&gt;&gt;xxx&gt;&gt;yyy&gt;&gt;xx&gt;&gt;yy;

//判断第一匹马的据点(xx,yy)
a[xxx][yyy]=1;
// P1
if(xxx+2&lt;=n&amp;&amp;yyy+1&lt;=m){
	a[xxx+2][yyy+1]=1;
}
// P2
if(xxx+1&lt;=n&amp;&amp;yyy+2&lt;=m){
	a[xxx+1][yyy+2]=1;
}
// P3
if(xxx-1&gt;=0&amp;&amp;yyy+2&lt;=m){
	a[xxx-1][yyy+2]=1;
}
// P4
if(xxx-2&gt;=0&amp;&amp;yyy+1&lt;=m){
	a[xxx-2][yyy+1]=1;
}
// P5
if(xxx-2&gt;=0&amp;&amp;yyy-1&gt;=0){
	a[xxx-2][yyy-1]=1;
}
// P6
if(xxx-1&gt;=0&amp;&amp;yyy-2&gt;=0){
	a[xxx-1][yyy-2]=1;
}
// P7
if(xxx+1&lt;=n&amp;&amp;yyy-2&gt;=0){
	a[xxx+1][yyy-2]=1;
}
// P8
if(xxx+2&lt;=n&amp;&amp;yyy-1&gt;=0){
	a[xxx+2][yyy-1]=1;
}

//判断第二匹马马的据点(xxx,yyy) 把(xx,yy)改成(xxx,yyy)即可 
a[xx][yy]=1;
// P1
if(xx+2&lt;=n&amp;&amp;yy+1&lt;=m){
	a[xx+2][yy+1]=1;
}
// P2
if(xx+1&lt;=n&amp;&amp;yy+2&lt;=m){
	a[xx+1][yy+2]=1;
}
// P3
if(xx-1&gt;=0&amp;&amp;yy+2&lt;=m){
	a[xx-1][yy+2]=1;
}
// P4
if(xx-2&gt;=0&amp;&amp;yy+1&lt;=m){
	a[xx-2][yy+1]=1;
}
// P5
if(xx-2&gt;=0&amp;&amp;yy-1&gt;=0){
	a[xx-2][yy-1]=1;
}
// P6
if(xx-1&gt;=0&amp;&amp;yy-2&gt;=0){
	a[xx-1][yy-2]=1;
}
// P7
if(xx+1&lt;=n&amp;&amp;yy-2&gt;=0){
	a[xx+1][yy-2]=1;
}
// P8
if(xx+2&lt;=n&amp;&amp;yy-1&gt;=0){
	a[xx+2][yy-1]=1;
}

dfs(0,0); 

cout&lt;&lt;sum;

return 0;

}

输入两匹马的位置都为（3，3）
结果仍然是6条路径

递归代码（双马）

用递归实现更简单
递归两匹马code：

#include<bits/stdc++.h>
using namespace std;
int main(){
int n,m,m1x,m1y,m2x,m2y,a[105][105],b[105][105]={0};
cin>>n>>m>>m1x>>m1y>>m2x>>m2y;
//马的据点
b[m1x][m1y]=1;
if(m1x-2>=0&&m1y-1>=0){
b[m1x-2][m1y-1]=1;
}
if(m1x-1>=0&&m1y-2>=0){
b[m1x-1][m1y-2]=1;
}
if(m1x+1<=n&&m1y-2>=0){
b[m1x+1][m1y-2]=1;
}
if(m1x+2<=n&&m1y-1>=0){
b[m1x+2][m1y-1]=1;
}
if(m1x+2<=n&&m1y+1<=m){
b[m1x+2][m1y+1]=1;
}
if(m1x+1<=n&&m1y+2<=m){
b[m1x+1][m1y+2]=1;
}
if(m1x-1>=0&&m1y+2<=m){
b[m1x-1][m1y+2]=1;
}
if(m1x-2>=0&&m1y+1<=m){
b[m1x-2][m1y+1]=1;
}</p>
<pre><code>b[m2x][m2y]=1;
if(m2x-2&gt;=0&amp;&amp;m2y-1&gt;=0){
	b[m2x-2][m2y-1]=1;
}
if(m2x-1&gt;=0&amp;&amp;m2y-2&gt;=0){
	b[m2x-1][m2y-2]=1;
}
if(m2x+1&lt;=n&amp;&amp;m2y-2&gt;=0){
	b[m2x+1][m2y-2]=1;
}
if(m2x+2&lt;=n&amp;&amp;m2y-1&gt;=0){
	b[m2x+2][m2y-1]=1;
}
if(m2x+2&lt;=n&amp;&amp;m2y+1&lt;=m){
	b[m2x+2][m2y+1]=1;
}
if(m2x+1&lt;=n&amp;&amp;m2y+2&lt;=m){
	b[m2x+1][m2y+2]=1;
}
if(m2x-1&gt;=0&amp;&amp;m2y+2&lt;=m){
	b[m2x-1][m2y+2]=1;
}
if(m2x-2&gt;=0&amp;&amp;m2y+1&lt;=m){
	b[m2x-2][m2y+1]=1;
}
//递归边界 
for(int i=0;i&lt;=m;i++){
	a[0][i]=1;
} 
for(int i=0;i&lt;=n;i++){
	a[i][0]=1;
}
//递归 
for(int i=1;i&lt;=n;i++){
	for(int j=1;j&lt;=m;j++){
		if(b[i][j]==0){
			a[i][j]=a[i-1][j]+a[i][j-1];
		}
	}
}
cout&lt;&lt;a[n][m]&lt;&lt;endl;

}

若有任何问题，欢迎在评论区留言！

以上！